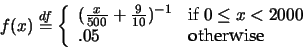


Next: Conclusion
Up: EMuds
Previous: Learning Classifier Systems
Subsections
In the preceding chapter, I have shown how the XCS system learns the
6-multiplexer problem. I want to show here that this learning ability
is a property that holds for this problem because of the regularities
that are compatible with the XCS system's representation and
generalization functionality (that I associate with information
compression). In the general case of a problem that is
not well understood and that must be solved, applying a particular
algorithm will help to understand the functionality and limits of the
algorithm, as well as the properties of the problem. I intend to show by
a trivial example that the representation of a problem plays a
fundamental role for adaptive behaviors and will relate this to the
question of information compression.
I have described previously why the multiplexer is used as a test case
for the XCS system. The multiplexer function is a boolean function,
which is naturally suited for learning by the use of classifiers; its
standard description is based on the use of an address set indexing a
value set that allows generalization to occur on individual bits
as patterns of zeroes and ones with wildcards. The term
``description'' that I use here should be understood as the symbolic
representation of input signals. The internal symbols used by
classifier systems as messages are strings of bits and the natural
symbol associated with an input signal is the bit string of the signal
itself, but other problems do not necessarily have such a ``natural''
mapping of inputs onto internal symbols.
For the multiplexer problems, the natural description is based on the
use that is made of the function by humans, but actually, the
description depends on perception of the problem by the system. And
the actual problem to solve is of distinguishing
inputs into two categories, those that are mapped to a one and those
that are mapped to a zero. The regularities of the function are simply
regularities of the description of this function. In the multiplexer
case, we use a description that is known to be expressive simply
because it is the one we use as humans to understand the problem and
associate an additional meaning to the order of the bits and their
signification. This proves to be a good description for a classifier
system to learn.
In the general case of a misunderstood problem, there is no guarantee
that the classifier system would obtain descriptions that are
compatible with its internal adaptation mechanisms. Imagine, for
example, that the multiplexer problem is described as a random
permutation of the input signals and that the XCS must learn this new
mapping. There will be no reason for it to be able to make good
generalizations if these permutations do not offer some degree of
compatible regularities (i.e. regularities over single bits in the
description).
By looking more attentively at the XCS classifier system applied to
this problem, there being only two levels of reward implied by the
input messages, the information content of an input message is only
one bit of information, distinguishing the reward options available to
the system when it chooses an action. The role of the algorithm is thus
to extract this information and use it to make a decision about the
amount of reward it has been programmed to choose. To this aim, the
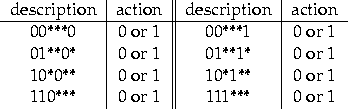
generalization mechanism of the XCS system finds a minimum of sixteen
general classifiers that resume this decision policy, the classifiers
shown on table 8.1. For each general condition, the
classifiers that advocate actions zero or one are accurate.
Obviously, this representation of the problem used is suboptimal,
since the only information content of an input string is one bit, but
it still is very close to an optimal representation.
Figure 8.1:
Complete family of 16 accurate maximally general classifiers.
 |
To illustrate the generalization capability of the XCS system, I have
used various permutations of the natural representation of the problem
and applied the classifier system to these new problems. In order to
give a quantitative measure of the distance between the original
description and the permutation over this basic description, five
types of permutations have been used. The permutations are of order 2 to
6, meaning that in permutations of order n, n interactions between
bits of the original description can be introduced (interactions in a
sense that can be related to the epistatic interactions as studied by
Kaufmann in [28]). The permutations are constructed in
the following way: n bits of the original representation are
swapped, then a random permutation over the n-dimensional space of
the selected bits is operated. As a result, the larger the n, the
further the descriptions provided to the classifier system are from the
original. When n=6, any function of
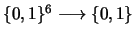 can be reached. Additionally, the permutation
leading to an optimal representation for the classifier system has
been used as a reference for the learning curves of the system. This
permutation can be obtained by mapping subspaces of the input space
onto a permuted description as described on table 8.2.
can be reached. Additionally, the permutation
leading to an optimal representation for the classifier system has
been used as a reference for the learning curves of the system. This
permutation can be obtained by mapping subspaces of the input space
onto a permuted description as described on table 8.2.
Figure 8.2:
An optimal permutation of the input signal.
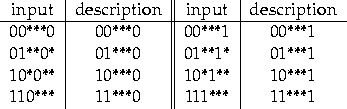 |
The inputs that match input patterns on the table are mapped to the
description patterns in the following column of the table. The
unspecified bits can be mapped to any other unspecified bit
position. For this permutation, all the information content of the
input that must be used to obtain a reward or not is contained in
the last bit of the description strings, so that the classifier system
can build a complete and accurate family of classifiers with only four
general classifiers in its population, those with conditions *****0 or
*****1 and actions 0 or 1. Other descriptions are optimal in this
sense, but due to the genetic search algorithm used to find new
classifiers, classifiers with longer defining lengths are slightly
suboptimal for crossover operations (defining length is the
distance between two specified positions in a pattern, for example the
pattern 01*00* has a defining length of 4 and the pattern *0100* a
defining length of 3).
For the experiments, one must be aware of the fact that the space of
all possible inputs to a function over 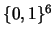 has 26=64different elements. Learning to map all the inputs correctly for a
reward function with just two levels requires twice that number of
specific classifiers or 128, when no generalization is used
(cf. tabular Q-Learning). For this problem, there are
36*2=1458different classifiers (including the general classifiers) available to
the system and, depending on the regularities in the function to be
learned, the minimal amount of classifiers needed to accurately learn
the function range between 128 in the worst case and 4 in the best
case. Therefore, whichever function the XCS must learn, if it is
allowed to have a population of more than 128 classifiers, it could
learn the function by using only specific classifiers. On the other
hand, if less that 128 classifiers are allowed in its population,
the function must have regularities that are compatible with the
generalization mechanism of the classifiers system, if the system is
to learn it correctly.
has 26=64different elements. Learning to map all the inputs correctly for a
reward function with just two levels requires twice that number of
specific classifiers or 128, when no generalization is used
(cf. tabular Q-Learning). For this problem, there are
36*2=1458different classifiers (including the general classifiers) available to
the system and, depending on the regularities in the function to be
learned, the minimal amount of classifiers needed to accurately learn
the function range between 128 in the worst case and 4 in the best
case. Therefore, whichever function the XCS must learn, if it is
allowed to have a population of more than 128 classifiers, it could
learn the function by using only specific classifiers. On the other
hand, if less that 128 classifiers are allowed in its population,
the function must have regularities that are compatible with the
generalization mechanism of the classifiers system, if the system is
to learn it correctly.
In the figures 8.3 to 8.5, I
illustrate the learning curves obtained for each order of permutation,
when the classifier population size allowed in the system is
400. The various curves show that with more interactions in between
the bits of the problem description, the learning ability of the
classifier system is reduced. In the optimal case where only one bit
sums up all the information about the function, the classifier system
quickly reaches 100% performance. The population diversity then
slowly reduces down to 25 individuals as the unnecessary classifiers
are eliminated by the genetic algorithm. The normal case is then only
slightly better than the learning of functions with order two
permutations from the normal description and we can see that each
increased permutation level introduces a degradation of the learning
ability of the system. Although this degradation is apparent, the
system still exhibits a good learning ability for these problems and
the prediction curves are still on a slight increase at the 10,000th
step. On the population curves, one sees that in each case, the
classifier system first generates a wide variety of classifiers, until
the 400 individuals limit is reached at 1300 steps. These
individuals are then evaluated and after the initial evaluation phase,
the inaccurate classifiers start to be eliminated from the population
and the overall population diversity gradually reduces to a minimal
amount of distinct types of classifiers. Except for the optimal
description case, the increase in population continues until about the
2000th step, where it reaches its peak (the overall population is now
400). In the optimal case, the elimination process is intense enough
to compensate the increase in population very early in the experiment.
In the figures 8.6 to 8.8, I
illustrate the learning curves obtained for each order of permutation,
when the classifier population size allowed in the system is
100. The number of steps considered here are 15,000. The optimal
problem description produces a function that can still be learned
Figure 8.3:
Prediction results of permutation experiments (pop. 400).
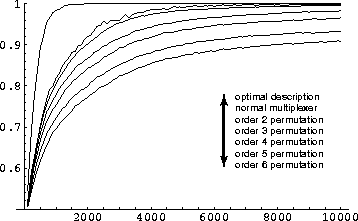 |
Figure 8.4:
Error results of permutation experiments (pop. 400).
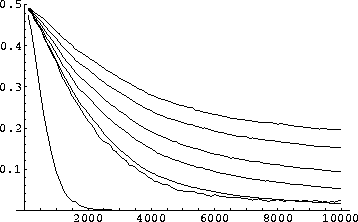 |
Figure 8.5:
Population results of permutation experiments (pop. 400).
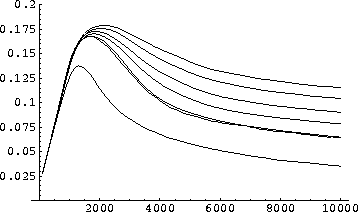 |
Figure 8.6:
Prediction results of permutation experiments (pop. 100).
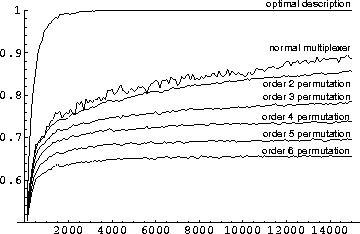 |
Figure 8.7:
Error results of permutation experiments (pop. 100).
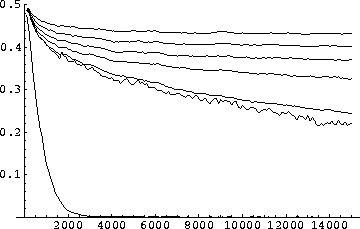 |
Figure 8.8:
Population results of permutation experiments (pop. 100).
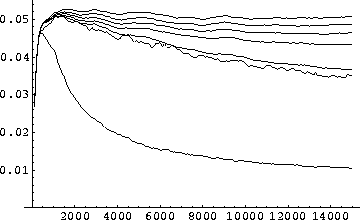 |
perfectly by the system after about 3000 steps, allowing the
population to be compressed to about 12 individual types. In the
other experiment, one can see that having only 100 individuals in
the population is problematic, although learning still occurs.
To explain this phenomenon, two reasons can be postulated. First of
all, the classifier system cannot
rely on a complete population of specific classifiers, this is a
problem that will always occur in more complex experiments and must be
coped with. The second reason is that although generalization would be
possible, the system would need more working space to hold various
classifiers as a genetic resource pool in addition to the accurate
classifiers useful for action selection. We see for example that the
number of different types of classifiers initially present in the
system is around 50, that is, the genetic algorithm produces an
average number of 50 different classifiers in a population of 100before the accuracy of these classifiers starts becoming
differentiated. In the different permutation experiments, this variety
is barely sufficient to differentiate the accuracies of the
classifiers in order for the system to start eliminating
classifiers. With the normal multiplexer problem and order two
permutation problems, this compression of the population can engage
and will eventually produce satisfactory results for learning the
function, but with permutations of a higher order, the population
compression stabilizes too fast for satisfactory learning of the
function. Still it is remarkable that even in the case of completely
random functions (order 6 permutations), the system is capable of
making correct decisions 60% of the time on average.
An optimal permutation that leaves the input information that is
relevant to the classifier system in the rightmost bit is shown in
table 8.2. Each one of the value bits that is addressed
by a particular configuration of the first two bits is simply swapped
with the rightmost bit (whatever its value). In this situation, the
XCS can learn only the position of this bit and generalize away all
the other bits, a situation for which I have plotted the learning
curves on figure 8.10. One notices here that the
number of steps until the system correctly predicts the choices that
must be made is much shorter since the number of general classifiers that
accurately describe the problem is reduced to a minimum of four. From
the step 1500 onwards, the classifier system always makes the correct
decision to maximize its reward and prediction error vanishes
completely from step 2000 on. The diversity of classifiers in the
population also reduces and stabilizes to 20 different types of
classifiers after 15 thousand steps.
Figure 8.9:
Results of the normal multiplexer: 10k and 30k steps.
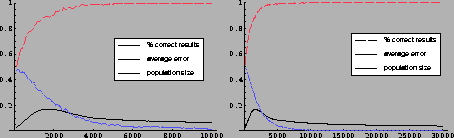 |
Figure 8.10:
Results of the optimal description problem: 10k and 30k steps.
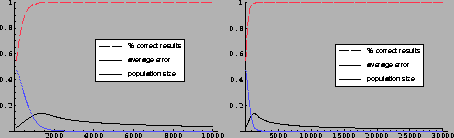 |
The objection that might be raised by this example is that by finding an optimal
description of the classifier inputs, one is in fact solving the
problem for the system and that there is no point in further
experimentation. This is precisely the point I am making, the
compression of information in the inputs to provide the system with a
description that is compatible with the functionality of the system is
the missing feature of this system and this feature is also missing
from most other adaptation algorithms that are used in AI. The
regularities of the environment have to be written in the terms of an
adaptation algorithm, here of the reward levels. In this problem,
the environment that is the space of input strings in standard form
has regularities that are not entirely detectable in terms of
the classifier system. But to the system, there are only two important
situations in the environment: those that provide a reward and those
that don't. Usually, the complexity of an environment is much larger
that what can be represented in a symbol system, but the situations
that are important to the system can be expressed much more simply in
the terms of that system. An algorithm that must deal with such
environments should be able to extract this information itself in
order to learn intelligent behaviors.
The preceding results have been produced by generating a number of
different test runs from random XCS system initializations. In the
simple experiments, the standard description of the multiplexer
problem and the optimal description of the multiplexer problem, 100
test runs were used to generate the averages plotted on the curves for
correct results, error in prediction and populations. In the
permutation experiments, 100 random permutations were generated for
each order of permutation and in each case 20 runs of the XCS system
were used to average the data, the overall averages are thus
calculated from 2000 test runs.
The number of classifiers allowed in the system were respectively 400
and 50 for the two different sets of experiments. With four hundred
individuals, the classifier system has sufficient resources to build
a complete representation of the problem space with specific
classifiers, although this will not usually happen since the
classifier system is driven towards generalization by its internal
mechanisms. With a population of 50 classifiers, the resources of the
system are not sufficient to cover all the problem space and the
system must be able to generalize in order to solve the problem.
The system parameters are the same as those given by Wilson in
[70], with his more recent clarifications about
implementation issues introduced: (available on
the Internet at http://world.std.com/ sw/imp-notes.html)
sw/imp-notes.html)
- rewards distributed for correct or incorrect answers of the
system are 1000 or 0 respectively
- the reinforcement parameters are:
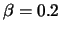 ,
,
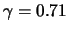 ,
,
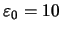 ,
,
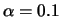 ,
,
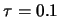
- the genetic algorithm based parameters are:
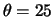 ,
,
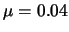 ,
,
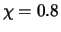 ,
,
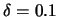 ,
,
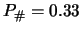
- initialization parameter for new classifiers were: strength =
10, error = 0, fitness = 0.01, experience = 0, covering
experience = 0 and match set size estimation = 0
Even though an XCS classifier system is seriously challenged when
having to learn the dynamics in an environment, a simple experiment
can be made, that shows the functional ability of the classifier
system to adapt to an environment where the causal role of actions
chosen is important. It was shown in the preceding experiment that the
generalization capabilities of the XCS system depend largely on the
coding of the information perceived, but that overall, the system is
able to generalize in a satisfactory manner (at least when the
information perceived is not too large). In this experiment, I want to
show that assuming the perceptions of the environment can be
generalized over, the system's ability to adapt to the dynamics of an
environment is not influenced very much by the description of this
environment.
The experiment that I have used to show this is of learning a simple
switch in the environment. Let me use the following informal
terminology for the description of the problem, the system used in the
experiment consists in:
- an agent: the (virtual) rat
- an agent: the cheesemaker
- a set of three connected rooms
- pieces of cheese
- rat ``traps''
In this system, the rat is the XCS agent that must learn to find and
eat pieces of cheese. The three rooms are aligned with a western room,
a central room and an eastern room each connected to its neighbor(s) by
one exit. The cheese maker is an automatic agent that starts in the
western room which is then empty. If the rat appears, he drops a piece
of cheese and a ``trap'', moves to the east, drops a ``trap'' and
moves to the east again, waiting in this eastern room until the rat
appears. If the rat enters the room, he drops a piece of cheese and
moves to the westernmost room, collecting the ``traps'' on his
way. The cycle then starts over. In the experiment, the ``traps'' have
no role other that to act as markers in the environment.
The rat agent must find a decision policy among four actions: moving
east, moving west, eating cheese, being inactive for a turn. The
sensory information he is provided with to make decisions consist in a string
of five true/false statements: is there an exit to the west, is there
an exit to the east, is there a trap here, is there a cheese maker
here and is there cheese here. His goal is to accurately and generally
associate each of the perception signals to one action. The
perceptions thus form a space of 32 different possibilities and the
possible classifiers in the system number 128. This problem,
although simple, requires the system to break out of the typical
looping behavior it is prone to enter when in a dynamic environment,
indeed, a classifier system has the tendency to enter two step
oscillations in such environments, since usually, one classifier
starts having maximal prediction value and accuracy in one room, and
then when moving to the next, another classifier will take over to
bring it back to the first room, creating a regular two step pattern.
Here, the system must adapt internally to an optimal chain of more
that two classifier choices, since the optimal behavior is to eat
cheese if some is available, move west when no trap is present and a
west exit exists or move east when an east exit is present and a trap
is present. This forces a set of a minimum of three general
classifiers to be found and maintained in the system. An XCS
classifier system has no memory (in the sense of internal memory
states), the way this problem must be learned by the system is through
the multi-step reinforcement procedure of the algorithm. This
multi-step reinforcement algorithm works by rewarding the classifiers
that advocated an action on a preceding step with the immediate
reward of that step and the discounted predictive value of the current
situation. Here, reward was given for eating food and no other action
was rewarded. The predictive value of moving or doing nothing is thus
only derived from the probability of finding cheese and eating it on
the next step, which leads to high levels of error value for the
movement or inaction classifiers.
Figure 8.11:
Results of the ``rat'' experiment (averages over 200 cases).
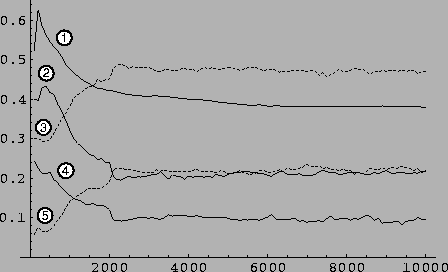 |
The results plotted here are those obtained by the situation described
above, with the same parameter values as in the multiplexer
problems. Since the goal of this experiment is not to find a perfect
(but maybe unstable solution), no parameter adjustment was used, even
though one can obtain almost perfect results by so doing. The result curves
are plotted on figure 8.11, with the number of action
cycles on the horizontal axis.
Curve (1) is the normalized number of distinct types of classifiers in
the XCS system, where a maximum population of 200 was allowed (.5means
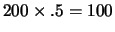 classifier types). Curves (2) to (5) are then
respectively the number of movements executed, the number of pieces of
cheese eaten, the failed attempts to act and the inactive steps of the
rat over the last hundred action cycles. In order to initialize the
system with an exploration phase, a function is used to
probabilistically allocate exploration and exploitation for
each step. The function used has decreasing values between zero and
one in the first two thousand steps and then stabilizes so that an
average of one action cycle in twenty is an exploration cycle. In
order to satisfy these criteria, the (somewhat arbitrary) function I
have used is:
classifier types). Curves (2) to (5) are then
respectively the number of movements executed, the number of pieces of
cheese eaten, the failed attempts to act and the inactive steps of the
rat over the last hundred action cycles. In order to initialize the
system with an exploration phase, a function is used to
probabilistically allocate exploration and exploitation for
each step. The function used has decreasing values between zero and
one in the first two thousand steps and then stabilizes so that an
average of one action cycle in twenty is an exploration cycle. In
order to satisfy these criteria, the (somewhat arbitrary) function I
have used is:
As can be seen on the graph 8.11, the population
diversity in classifier types exhibits a similar behavior as in the
multiplexer experiments, sharply rising at first and then reducing as
accurate general classifiers are progressively found for the
problem. This population stabilizes at around 80 distinct varieties
of classifiers which is quite a large amount, given the maximum of
128 possibilities and the fact that only 4 should suffice to sum
up the solution to the problem. The curves numbered (3) to (5) then
represent the total actions of each type that the system uses to solve
the problem (move, eat, do nothing). Since each action is equally
likely to occur at the beginning of the experiment, there are about
double the amount of moves as eat or ``noop'' actions. The initial
differences reside in the fact that choosing to be inactive never
fails, whereas choosing to eat will fail every time there is no food in
the current locus. The last curve (4) is the number of failed attempts
to do something, such as moving east when there is no east exit or
eating when there is no food. Curves (2) to (5) sum up to 1 at each
stage.
Figure 8.12:
Results of the ``rat'' permutation experiments.
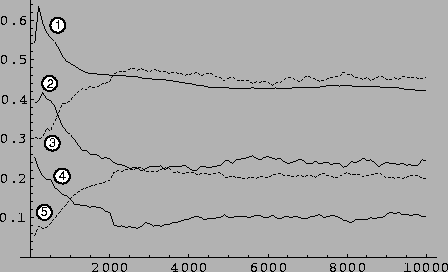 |
As illustrated, the system is able to find an equilibrium between the
number of moves at each stage and the number of pieces of cheese
eaten, the fact that the moves stabilize to about double the amount of
pieces of cheese eaten indicate that the algorithm never oscillates
between two neighbor locations, moving to the extremities of the
environment at each passage. The failed attempts can then be accounted
for by the fact that the agent then pushes on, trying to move further
until the failed attempts (there is no east exit to move through in
the eastern room) bring the predictive value of moving in that
direction lower than that of moving in the other direction. Overall,
this behavior is a good attempt at modeling the switching function of
the problem, without the expressive ability to have a better
approximation of the problem solution. With some changes in the
parameters of the algorithm, it should be possible to minimize the
failed attempts phase of this solution, but I have not investigated
the matter in detail. The point that I want to make is that we can see
here the way in which the classifier system attempts to express the
dynamics of the environment within its own limited expressive
capability.
In the multiplexer experiments, the full information about the problem
could be stored in terms of stable classifier predictions, with
accuracy indicating whether a classifier was a good description of an
environment regularity or not. Here, the information that must be
acquired by the system is not static and each classifier does not have
a definitive predictive value. Instead, predictive values will change
over time for some classifiers, depending on the current situation of the
agent: the full information for the problem resides in multiple
step evaluations. For an XCS to capture this, it must still store the
information in the classifiers, but most of this information is now
held by the prediction, error and accuracy values of these
classifiers, since the predictions now have a continuous range of
possible values that dynamically vary from situation to situation. The
characterization of the system's functionality now depends much less
on its ability to generalize over the input perceptions of the system,
than on its ability to express the dynamics of the problem in the
predictive values of the classifiers.
To highlight this, I have reproduced the same experiment, but with
other perceptual descriptions of the environment. As in the
multiplexer problems, I have coded the perceptual inputs from the
environment by using random permutations of the input space. When this
is done, the XCS system must generalize its representation of the
world in terms of classifiers, but without the same regularities in
the inputs. The data for these experiments (averaged over 200 sample
random permutations) show that although the diversity of classifiers
in the population is affected (it increases), the solution to the
problem that is found by the algorithm gives the same results. The
global results are shown on figure 8.12, while the
comparative results are shown on figures 8.13 and
8.14.
Figure 8.13:
Comparative results, moves and eating.
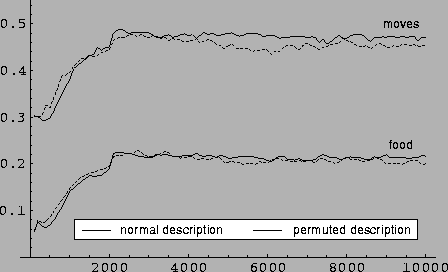 |
Figure 8.14:
Comparative results, population, failed actions and ``noops''.
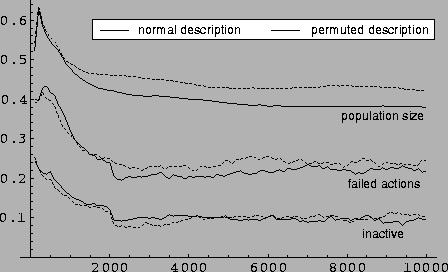 |
Clearly, the perception of the environment affects the classifier
system in its operation, but this effect is limited to the
representational ability of the system and not the way in which it can
learn the dynamics of the environment.
The two experiments described in this chapter show that information
compression (in the sense of generalization for a classifier system)
is an essential feature of an agent algorithm that must learn in rich
environments. Every algorithm developed in the field of AI for such
agents is capable of some form of generalization, be it implicit or
explicit. What differs from system to system is the internal structure
and functions in which this information compression is expressed. It
is this language of representation that characterizes an algorithm.
As we have seen in the preceding experiments, there is a range of
problems that can naturally be addressed by a classifier system, and
others that simply are not adapted to such systems. This expressivity
factor is fundamental when choosing an algorithm to solve a problem
and is already intuitively understood by most scientists, but has not
been formalized as I find necessary: when attempting to solve real
world problems, a connectionist approach is often chosen for its
``continuity'' properties and when a modern expert system is
implemented a symbolic approach is preferred, but no precise
characterization of the relevant properties of each system has been
attempted. Since every problem has a distinct type of regularities
that must be integrated by agents programmed to solve them, I would
like to propose that it is now time for AI researchers to
focus on a classification of algorithms, based on their generalization
capabilities and internal dynamics.



Next: Conclusion
Up: EMuds
Previous: Learning Classifier Systems
Antony Robert
2000-02-11

![]() can be reached. Additionally, the permutation
leading to an optimal representation for the classifier system has
been used as a reference for the learning curves of the system. This
permutation can be obtained by mapping subspaces of the input space
onto a permuted description as described on table 8.2.
can be reached. Additionally, the permutation
leading to an optimal representation for the classifier system has
been used as a reference for the learning curves of the system. This
permutation can be obtained by mapping subspaces of the input space
onto a permuted description as described on table 8.2.
![]() has 26=64different elements. Learning to map all the inputs correctly for a
reward function with just two levels requires twice that number of
specific classifiers or 128, when no generalization is used
(cf. tabular Q-Learning). For this problem, there are
36*2=1458different classifiers (including the general classifiers) available to
the system and, depending on the regularities in the function to be
learned, the minimal amount of classifiers needed to accurately learn
the function range between 128 in the worst case and 4 in the best
case. Therefore, whichever function the XCS must learn, if it is
allowed to have a population of more than 128 classifiers, it could
learn the function by using only specific classifiers. On the other
hand, if less that 128 classifiers are allowed in its population,
the function must have regularities that are compatible with the
generalization mechanism of the classifiers system, if the system is
to learn it correctly.
has 26=64different elements. Learning to map all the inputs correctly for a
reward function with just two levels requires twice that number of
specific classifiers or 128, when no generalization is used
(cf. tabular Q-Learning). For this problem, there are
36*2=1458different classifiers (including the general classifiers) available to
the system and, depending on the regularities in the function to be
learned, the minimal amount of classifiers needed to accurately learn
the function range between 128 in the worst case and 4 in the best
case. Therefore, whichever function the XCS must learn, if it is
allowed to have a population of more than 128 classifiers, it could
learn the function by using only specific classifiers. On the other
hand, if less that 128 classifiers are allowed in its population,
the function must have regularities that are compatible with the
generalization mechanism of the classifiers system, if the system is
to learn it correctly.
![]() sw/imp-notes.html)
sw/imp-notes.html)